Finder
Veteran
I have been having a very interesting conversation about mathematical perspective offline with one of our members since this thread began. And I think I have found the missing factor that people have been overlooking in this debate.
I was shown an image of my brick building with the crop superimposed over the original and showing they both share the same vanishing points. If both images share the same vanishing points, then both images have the same perspective.
But the illustration was not correct.
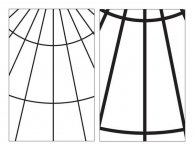
The comparison between the original and crop are done at the same size. The crop is enlarged to match the original. The change in magnification displaces the linear features so the two images do not share the same set of vanishing points anymore. And if two image have different vanishing points, they have different perspectives. Since the displacement would always be away from the original, perspective becomes weaker. This is also evident in the example illustrations I have been posting.
So cropping or changing focal length will be enough to change perspective.
I was shown an image of my brick building with the crop superimposed over the original and showing they both share the same vanishing points. If both images share the same vanishing points, then both images have the same perspective.
But the illustration was not correct.
The comparison between the original and crop are done at the same size. The crop is enlarged to match the original. The change in magnification displaces the linear features so the two images do not share the same set of vanishing points anymore. And if two image have different vanishing points, they have different perspectives. Since the displacement would always be away from the original, perspective becomes weaker. This is also evident in the example illustrations I have been posting.
So cropping or changing focal length will be enough to change perspective.
Attachments
Last edited:
Finder
Veteran
Apparently, this does not apply to fields using mathematical perspective and the two image would still be regarded as having the same perspective. However, in photography, which is interested in the perception of space rather than any absolute qualities, this does illustrate that the viewer would perceive a change in perspective. This is also evident in the other examples I gave.
You can get definitions of perspective in photography and the factors involved in The focal Encyclopedia of Photography and Materials and Processes of Photography if you would like to find out about this.
You can get definitions of perspective in photography and the factors involved in The focal Encyclopedia of Photography and Materials and Processes of Photography if you would like to find out about this.
Jeicob
Amateur
Roger Hicks
Veteran
A mathematical model of perspective is about as meaningful as a mathematical model in economics.
Cheers,
R.
I have to argue that a mathematical model of perspective is fairly deterministic. The projection of a 3-D model onto a 2-D plane using the position of the observer in the computation is straight-forward. But that was the 1980s for me, in FORTRAN of course.
I saw an economics model based on Fourier Transforms, paying attention to "Kondratieff long wave cycles". I do not think that is deterministic.
But for perspective in photography- not so easy. Easy in computer generated images.
I saw an economics model based on Fourier Transforms, paying attention to "Kondratieff long wave cycles". I do not think that is deterministic.
But for perspective in photography- not so easy. Easy in computer generated images.
Last edited:
blackwave
silver halide lover
This thread is frustrating to read! The location of your eyes is what changes perspective, nothing else. The "compression" and "stretching" of perspective relies entirely on where your camera is located. A given focal length does *not* inherently show a certain perspective like the original post suggests.
If you put a 15mm lens on a small enough format it's going to look like a super-mega-omg-telephoto. If you put a 1000mm lens on a large enough format it's going to look like a mind-bending-omg-fisheye... depending on where you stand, of course.
If you put a 15mm lens on a small enough format it's going to look like a super-mega-omg-telephoto. If you put a 1000mm lens on a large enough format it's going to look like a mind-bending-omg-fisheye... depending on where you stand, of course.
Finder
Veteran
My illustration was a bad attempt at showing simple converging lines representing perspective (if you were not looking up, they would be parallel). I placed the curves as I wanted to see how the arch would be represented.
And now you know why I did not go into graphic design.
Last edited:
aizan
Veteran
re: the magic window
somebody said that if a 15mm (on 135 format) looks wide, you're just not standing close enough to the print!
somebody said that if a 15mm (on 135 format) looks wide, you're just not standing close enough to the print!
Frankie
Speaking Frankly
I spent my life long career dealing with just this problem...it is called analytical photogrammetry. And you are right, it is straight forward...except for the untrained.
And I "never had a lesson" in FORTRAN.
As I previously wrote:
"The native FoV, a property of the lens, does not change.
The effective FoV depends on cropping...at the sensor or in wet-printing.
Perspective is a function of camera-to-subject distance, given a focal length.
Perspective will be different when one changes camera-to-subject distance [steps back] or focal length [to shorter] to regain effective FoV lost to sensor crop-factor.
[There is a body of mathematics defining the above in my field...predating "crop-factor" talk by about 4 decades.]
I think it is the talk of "35mm [format] equivalent focal length" prevalent in digital camera reviews that confuses most."
Last edited:
back alley
IMAGES
what are we mere mortals to do?
Chris101
summicronia
Are you suggesting that the native field of view is dependent solely on the focal length of the lens used? I can't possibly see how that can be. A Sigma 90mm macro lens for 35mm cameras has the exact same focal length as a 90mm superangulon for large format. Yet the native field of view of the two lenses is very different. The sigma will project an image that is about two inches in diameter, while the superangulon's image circle will be about a foot across.
Surely, we must only be talking about the effective field of view when we argue about the meaning of perspective.
I cannot see how the perspective will change if I shoot a scene with a 52mm on a 35mm camera (A Konica no doubt, because their normal lens was labeled 52mm), or with a 35mm on a Nikon D2x (or other 1.5x crop camera.) Focal length seems to have absolutely no effect on the appearance of the picture in this case.
Last edited:
Frankie
Speaking Frankly
I never said all lenses of a given [or labeled] focal length [independent of format] will or must have the same native FoV. Some lenses, particularly those designed for [larger format] view cameras, have wider FoV or larger "image circle" to support camera movements.
The effective FoV [of a lens] is just that...the amount cropped by the image format/frame. Tilt/shift lenses in 35mm format are also good examples...as are digital cameras with crop factors.
In photogrammetry, all that is conceptualized as a "bundle of light rays gathered through a perspective centre"...as if the lens only has a single focal point located at the focal length [distance]. The portion cropped by the image format thus contains a bundle set with a fixed range of incident angles...from zero in the centre [principal point] to the widest in corners.
In each bundle set gathered [exposure], changes in imaging distance will result in changing apparent object displacement [or leans, radially away from the principal point...as in the pin-cushion effect]. OR, if a shorter lens focal length is used [perspective centre closer to image plane], every incident angle in the bundle set will change...except only at the principal point, and increasingly more pronounced outward. All effects are measurable if not apparent.
Crop factors in digital cameras either cause you to step back [increase imaging distance] or use a shorter focal length to achieve a given FoV...hence causing perspective changes.
Last edited:
Finder
Veteran
Go out. Take pictures. And if you like what you see, be happy with it.
Frankie
Speaking Frankly
I agree with Finder. Just go out and take pictures with whatever focal length lens that pleases you.
Pico
-
Thanks, Brian Hayden and others. Critique and correction is appreciated. The comments I wrote came from an academic who had me rather convinced. I'd rather be in doubt than certain. It is something about the wisdom of insecurity.
Jeicob: How did you do that fill-in?
--
Pico in SE Minnesota
Jeicob: How did you do that fill-in?
--
Pico in SE Minnesota
Last edited:
Pico
-
Last edited:
Chris101
summicronia
Please excuse me for being dense and for editing my quote of your comment, but I still don't see how this is so.
antiquark
Derek Ross
The only thing that will change the perspective is walking closer to, or farther from, the scene. (A.k.a. footzoom).
Altering the focal length will do nothing to perspective.
Altering the focal length will do nothing to perspective.
Roger Hicks
Veteran
Dear Derek,
OR printing bigger or smaller, or varying the distance from which you look at the print.
And there are other kinds of perspective...
Cheers,
R.
Finder
Veteran
Which is why all the pictures I take with my Horseman SW612 and 55mm lens look exactly like the pictures from my Mamiya 6 with a 75mm lens.